Table Of Content
I have a Master of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations. Unfortunately nuisance variables often arise in experimental studies, which are variables that effect the relationship between the explanatory and response variable but are of no interest to researchers. In the first example provided above, the sex of the patient would be a nuisance variable.
Introduction to Probability and Statistics
In an RCBD, we can estimate any treatment contrast and all effects independently within each block, and then average over blocks. We can use the same intra-block analysis for a BIBD by estimating contrasts and effects based on those blocks that contain sufficient information and averaging over these blocks. We can see in the table below that the other blocking factor, cow, is also highly significant. The degrees of freedom for error grows very rapidly when you replicate Latin squares. But usually if you are using a Latin Square then you are probably not worried too much about this error.
Probability for Data Science
It typically deteriorates if the block size becomes too large, since experimental units then become more heterogeneous. A balanced incomplete block design allows blocking of simple treatment structures if only a subset of treatments can be accommodated in each block. The latin square design requires identical number of levels for the row and column factors.
Book traversal links for 8.9 - Randomized Block Design: Two-way MANOVA
To this end, we arrange (or block) mice into groups of three and randomize the drugs separately within each group, such that each drug occurs once per group. Ideally, the variance between animals in the same group is much smaller than between animals in different groups. A common choice for blocking mice is by litter, since sibling mice often show more similar responses as compared to mice from different litters (Perrin 2014). Litter sizes are typically in the range of 5–7 animals in mice (Watt 1934), which would easily allow us to select three mice from each litter for our experiment. Latin Square Designs are probably not used as much as they should be - they are very efficient designs. In other words, these designs are used to simultaneously control (or eliminate) two sources of nuisance variability.
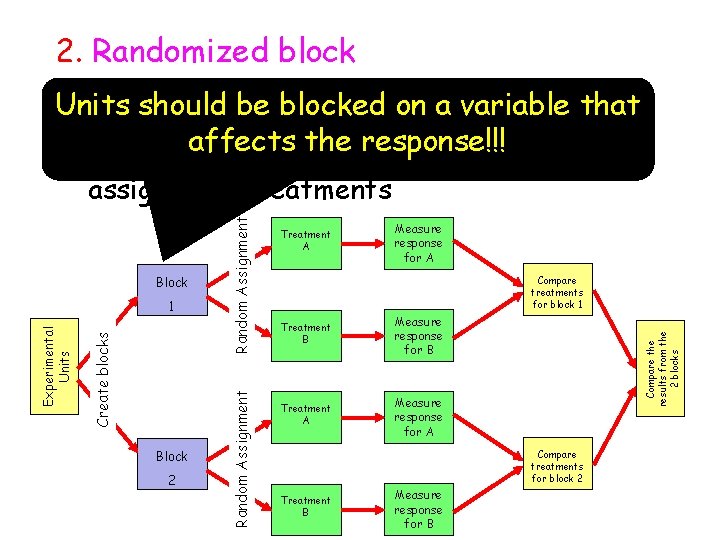
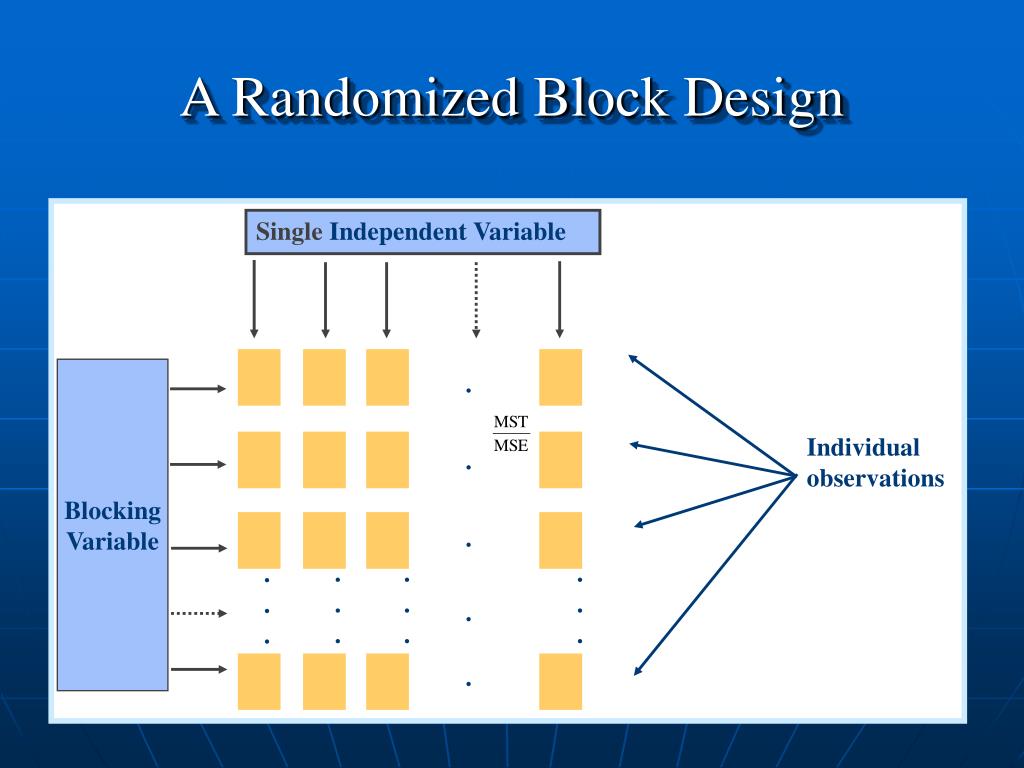
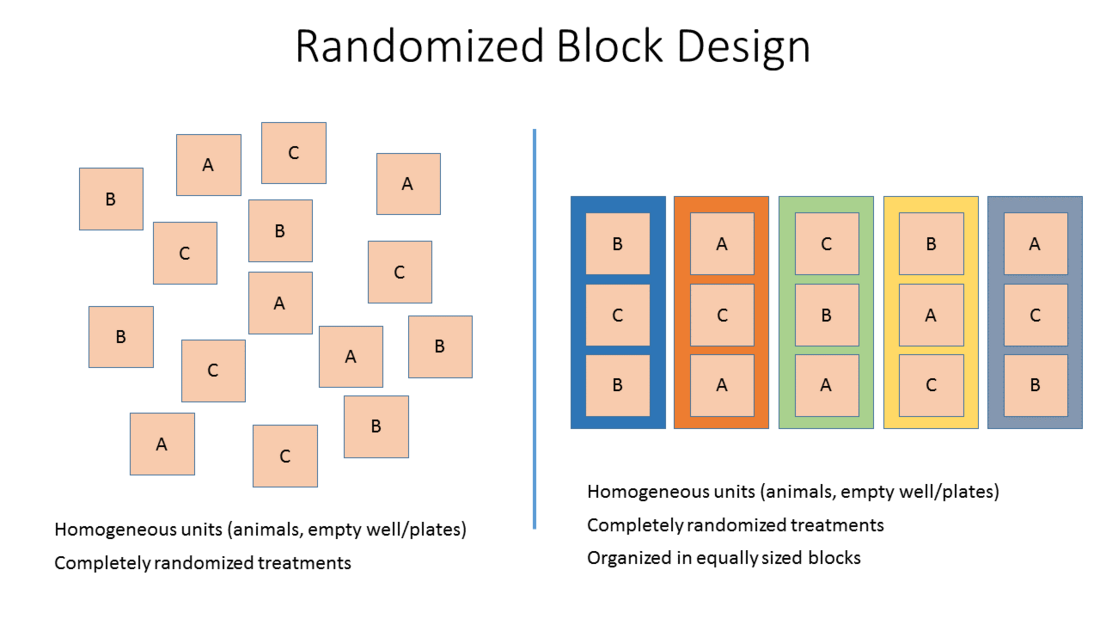
We can determine whether cell phone use has an effet on driving ability after controlling for driving experience. In randomized block design, the control technique is done through the design itself. First the researchers need to identify a potential control variable that most likely has an effect on the dependent variable. Researchers will group participants who are similar on this control variable together into blocks. This control variable is called a blocking variable in the randomized block design. The purpose of the randomized block design is to form groups that are homogeneous on the blocking variable, and thus can be compared with each other based on the independent variable.
Statistical Methods for Data Science
With missing data or IBDs that are not orthogonal, even BIBD where orthogonality does not exist, the analysis requires us to use GLM which codes the data like we did previously. For an odd number of treatments, e.g. 3, 5, 7, etc., it requires two orthogonal Latin squares in order to achieve this level of balance. For even number of treatments, 4, 6, etc., you can accomplish this with a single square. This form of balance is denoted balanced for carryover (or residual) effects. For instance, we might do this experiment all in the same factory using the same machines and the same operators for these machines.
Field Study in Statistics
Students interested in teaching statistics and mathematics in middle or high school should pursue the teaching option within the major. Students interested in teaching should also consider the Cal Teach Program. To achieve replicates, this design could be replicated several times.
To improve the precision of treatment comparisons, we can reduce variability among the experimental units. We can group experimental units into blocks so that each block contains relatively homogeneous units. However it would be pretty sloppy to not do the analysis correctly because our blocking variable might be something we care about.
In this experiment, we are interested in contrasting the plates on the same patients, not the patients themselves. The ten plates are then the treatment factor levels, and each patient is a block to which we assign plates. Since \(\lambda\) is not an integer there does not exist a balanced incomplete block design for this experiment. Seeing as how the block size in this case is fixed, we can achieve a balanced complete block design by adding more replicates so that \(\lambda\) equals at least 1. It needs to be a whole number in order for the design to be balanced. It looks like day of the week could affect the treatments and introduce bias into the treatment effects, since not all treatments occur on Monday.
Integrative web cloud computing and analytics using MiPair for design-based comparative analysis with paired ... - Nature.com
Integrative web cloud computing and analytics using MiPair for design-based comparative analysis with paired ....
Posted: Mon, 28 Nov 2022 08:00:00 GMT [source]
Notice that in our block level, there is no p-value to assess if the blocks are different. So our analysis respects that blocks are present, but does not attempt any statistical analyses on them. Fortunately in this case, we don’t care about the blocking variable and including it in the model was simply guarding us in case there was a difference, but I wasn’t interested in estimating it. If the only covariate we care about is the most deeply nested effect, then we can do the usual analysis and recognize the p-value for the blocking variable is nonsense, and we don’t care about it.
In the previous example, gender was a known nuisance variable that researchers knew affected weight loss. By placing the individuals into blocks, the relationship between the new diet and weight loss became more clear since we were able to control for the nuisance variable of gender. No major is complete without encountering the fields that interface closely with statistics. The minor is for students who want to study a significant amount of statistics and probability at the upper division level. For information regarding the requirements, please see the Minor Requirements tab on this page. Since the first three columns contain some pairs more than once, let's try columns 1, 2, and now we need a third...how about the fourth column.
Often in medical studies, the blocking factor used is the type of institution. Sometimes several sources of variation are combined to define the block, so the block becomes an aggregate variable. Consider a scenario where we want to test various subjects with different treatments.
When the data are complete this analysis from GLM is correct and equivalent to the results from the two-way command in Minitab. What if the missing data point were from a very high measuring block? It would reduce the overall effect of that treatment, and the estimated treatment mean would be biased. Basic residual plots indicate that normality, constant variance assumptions are satisfied. Therefore, there seems to be no obvious problems with randomization. These plots provide more information about the constant variance assumption, and can reveal possible outliers.
Each block then contains one full replicate of the factorial design, and the required block size rapidly increases with the number of factors and factor levels. In practice, only smaller factorials can be blocked by this method since heterogeneity between experimental units often increases with block size, diminishing the advantages of blocking. We discuss more sophisticated designs for blocking factorials that overcome this problem by using only a fraction of all treatment combinations per block in Chapter 9. Finally, we might use the same row and column factor levels in each replicate.
No comments:
Post a Comment